Pi est la constante correspondant au rapport de la circonférence du cercle à la longueur de son diamètre. Dans la pratique courante, on utilise généralement sa valeur approchée par défaut c'est à dire 3,14.
Pourtant depuis des siècles ce nombre n'a cessé d'intriguer les chercheurs. L'étude approfondie de ce nombre et de ses décimales nous révèle des surprises inattendues, d'étranges synchronicités, qui nous amèneront aux portes de l'Inconnu. Etudier le "Code Pi", c'est un peu comme si on tentait de déchiffrer une sorte de langage mathématique universel et transcendant.
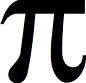 est un nombre qui a fasciné tant de savants depuis l'antiquité. Si ce nombre remporte un tel succès, c'est d'abord parce qu'il recèle des propriétés passionnantes, mais surtout c'est sa nature qui en fait un nombre d'exception.
est un nombre qui a fasciné tant de savants depuis l'antiquité. Si ce nombre remporte un tel succès, c'est d'abord parce qu'il recèle des propriétés passionnantes, mais surtout c'est sa nature qui en fait un nombre d'exception.
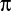 est un nombre irrationnel, c'est à dire qu'il s'écrit avec un nombre infini de décimales sans suite logique.
est un nombre irrationnel, c'est à dire qu'il s'écrit avec un nombre infini de décimales sans suite logique.
On qualifiera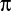 de nombre de "transcendant". La transcendance de
de nombre de "transcendant". La transcendance de 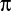 établit l'impossibilité de résoudre le problème de la quadrature du cercle : il est impossible de construire, à l'aide de la règle et du compas seulement, un carré dont la surface est rigoureusement égale à la surface d'un disque donné.
établit l'impossibilité de résoudre le problème de la quadrature du cercle : il est impossible de construire, à l'aide de la règle et du compas seulement, un carré dont la surface est rigoureusement égale à la surface d'un disque donné.

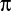 : chaque pixel représente une décimale.
: chaque pixel représente une décimale.
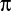 . Le nombre de lettres de chaque mot coïncide dans le même ordre avec une décimale de
. Le nombre de lettres de chaque mot coïncide dans le même ordre avec une décimale de 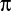 . Un nombre à 10 lettres correspond au chiffre 0.
. Un nombre à 10 lettres correspond au chiffre 0.
Que(3) j(1)'aime(4) à(1) faire(5) apprendre ce nombre utile aux sages !
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur ?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l'admirable procédé, l'oeuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l'espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s'y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l'orbe calculée approchera ;
Définira limite ; enfin, l'arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.
 En 2010, un japonais et un américain ont calculé cinq mille millards de décimales du nombre pi, soit près du double du record précédent établi en décembre 2009. Dans Star Trek, en 1967, le capitaine Kirk et Monsieur Spock avaient ordonné à l'ordinateur de l'Enterprise de calculer le nombre pi jusqu'à sa dernière décimale. Une manière de provoquer un calcul infini, pour chasser l'alien qui s'était emparé de la machine. Au printemps 2010, le Japonais Shigeru Kondo donne un ordre similaire à son PC de bureau, équipé d'un programme conçu par un étudiant de 22 ans, l'Américain Alexander Yee, rencontré via Internet. Trois mois plus tard, le 2 août, le duo annonce un nouveau record à battre : cinq mille milliards de décimales de pi.
En 2010, un japonais et un américain ont calculé cinq mille millards de décimales du nombre pi, soit près du double du record précédent établi en décembre 2009. Dans Star Trek, en 1967, le capitaine Kirk et Monsieur Spock avaient ordonné à l'ordinateur de l'Enterprise de calculer le nombre pi jusqu'à sa dernière décimale. Une manière de provoquer un calcul infini, pour chasser l'alien qui s'était emparé de la machine. Au printemps 2010, le Japonais Shigeru Kondo donne un ordre similaire à son PC de bureau, équipé d'un programme conçu par un étudiant de 22 ans, l'Américain Alexander Yee, rencontré via Internet. Trois mois plus tard, le 2 août, le duo annonce un nouveau record à battre : cinq mille milliards de décimales de pi.
Pourtant depuis des siècles ce nombre n'a cessé d'intriguer les chercheurs. L'étude approfondie de ce nombre et de ses décimales nous révèle des surprises inattendues, d'étranges synchronicités, qui nous amèneront aux portes de l'Inconnu. Etudier le "Code Pi", c'est un peu comme si on tentait de déchiffrer une sorte de langage mathématique universel et transcendant.
Nature de Pi
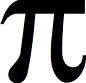 est un nombre qui a fasciné tant de savants depuis l'antiquité. Si ce nombre remporte un tel succès, c'est d'abord parce qu'il recèle des propriétés passionnantes, mais surtout c'est sa nature qui en fait un nombre d'exception.
est un nombre qui a fasciné tant de savants depuis l'antiquité. Si ce nombre remporte un tel succès, c'est d'abord parce qu'il recèle des propriétés passionnantes, mais surtout c'est sa nature qui en fait un nombre d'exception.
On qualifiera
Art et Concept
L'image ci-contre est une représentation du nombrePoésie et Géométrie
Le poème qui suit permet de retenir les premières décimales deQue(3) j(1)'aime(4) à(1) faire(5) apprendre ce nombre utile aux sages !
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur ?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l'admirable procédé, l'oeuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l'espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s'y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l'orbe calculée approchera ;
Définira limite ; enfin, l'arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.
Dernier record
 En 2010, un japonais et un américain ont calculé cinq mille millards de décimales du nombre pi, soit près du double du record précédent établi en décembre 2009. Dans Star Trek, en 1967, le capitaine Kirk et Monsieur Spock avaient ordonné à l'ordinateur de l'Enterprise de calculer le nombre pi jusqu'à sa dernière décimale. Une manière de provoquer un calcul infini, pour chasser l'alien qui s'était emparé de la machine. Au printemps 2010, le Japonais Shigeru Kondo donne un ordre similaire à son PC de bureau, équipé d'un programme conçu par un étudiant de 22 ans, l'Américain Alexander Yee, rencontré via Internet. Trois mois plus tard, le 2 août, le duo annonce un nouveau record à battre : cinq mille milliards de décimales de pi.
En 2010, un japonais et un américain ont calculé cinq mille millards de décimales du nombre pi, soit près du double du record précédent établi en décembre 2009. Dans Star Trek, en 1967, le capitaine Kirk et Monsieur Spock avaient ordonné à l'ordinateur de l'Enterprise de calculer le nombre pi jusqu'à sa dernière décimale. Une manière de provoquer un calcul infini, pour chasser l'alien qui s'était emparé de la machine. Au printemps 2010, le Japonais Shigeru Kondo donne un ordre similaire à son PC de bureau, équipé d'un programme conçu par un étudiant de 22 ans, l'Américain Alexander Yee, rencontré via Internet. Trois mois plus tard, le 2 août, le duo annonce un nouveau record à battre : cinq mille milliards de décimales de pi.
















 Centre d'Aide
Centre d'Aide Alertes
Alertes Amis
Amis Blog
Blog Écologie
Écologie Glossaire
Glossaire Gradation
Gradation Livre d'Or
Livre d'Or Radios
Radios Services
Services Time Line
Time Line Univers
Univers Youtube
Youtube Groupes
Groupes
